I solidi. - ppt video online scaricare
Di uno scrittore di uomini misteriosi
Last updated 29 maggio 2024
FAI UN CLIC CON IL TASTO SINISTRO DEL MOUSE CLASSIFICAZIONE DELLE FIGURE SOLIDE PER ANDARE AVANTI FAI UN CLIC CON IL TASTO SINISTRO DEL MOUSE
CLASSIFICAZIONE. DELLE FIGURE SOLIDE. PER ANDARE AVANTI. FAI UN CLIC CON IL TASTO SINISTRO DEL MOUSE.
Osserva i solidi geometrici disegnati. sfera. POLIEDRI. Se consideriamo le loro facce. alcuni solidi sono limitati da SUPERFICI PIANE. alcuni da SUPERFICI PIANE e da SUPERFICI CURVE. uno di essi da una sola SUPERFICIE CURVA : la sfera. Circondiamo con una linea rossa tutti i solidi delimitati solamente da facce piane. Abbiamo formato l’insieme dei POLIEDRI.
Quelli che hanno una sola base di appoggio: le PIRAMIDI. Quelli che hanno due basi di appoggio CONGRURENTI e PARALLELE. Circondiamo con una linea rossa tutti i poliedri che hanno. due basi congruenti e parallele. Abbiamo formato l’insieme dei PRISMI.
I PRISMI. PARALLELEPIPEDI. Circondiamo con una linea rossa tutti i prismi che hanno per basi dei parallelogrammi. Abbiamo formato l’insieme dei PARALLELEPIPEDI.
SOLIDI GEOMETRICI. POLIEDRI. NON POLIEDRI. PIRAMIDI. PRISMI. PARALLELEPIPEDI. CUBO.
I solidi che hanno superfici curve vengono chiamati solidi rotondi.
Si dice poliedro un solido delimitato da poligoni, situati su piani diversi e disposti in modo che ognuno dei lati sia comune a due di essi. I poligoni si dicono facce del poliedro; i loro lati si dicono spigoli del poliedro. due facce con uno spigolo comune si dicono facce adiacenti. i loro vertici si dicono vertici del poliedro;
LA PARABOLA E LA SUA EQUAZIONE. /15. DEFINIZIONE. Poliedro. Un poliedro è una figura solida limitata da un numero finito di poligoni appartenenti a piani diversi e tali che il piano di ogni poligono non attraversi il solido. Prisma. La distanza fra il vertice (o la base superiore) e il piano della base (inferiore) si chiama altezza. L’altezza delle facce laterali di una piramide retta è detta apotema. Piramide. 9.
LA PARABOLA E LA SUA EQUAZIONE. /15. DEFINIZIONE. Poliedro regolare. Un poliedro si dice regolare quando le sue facce sono poligoni regolari congruenti e anche i suoi angoloidi e i suoi diedri sono congruenti. DEFINIZIONE. Solido di rotazione. Si chiama solido di rotazione un solido generato dalla rotazione di una figura piana intorno a una retta r. 10.
Osserviamo il poliedro della figura a fianco. Indichiamo con: • V il numero dei vertici. • F il numero delle facce. • S il numero degli spigoli. Osserviamo che per tutti i poliedri vale la seguente relazione: Relazione di Eulero. V + F − S = 2. o anche V + F = S + 2.
I vertici sono 12 e le facce 8. Sostituiamo i numeri che conosciamo nella relazione di Eulero: V + F = S = S + 2. Il numero degli spigoli è: S = − 2 = 18. Prova tu. • Quanti spigoli ha un poliedro con 6 facce e 8 vertici ……………………………. V + F = S + 2. S = V + F − 2 S = − 2 = 12. Il poliedro ha 12 spigoli.
Si chiama prisma un poliedro delimitato da due poligoni congruenti, detti basi, situati su piani paralleli e da tanti parallelogrammi quanti sono i lati di ciascuno dei due poligoni. pentagonale. quadrangolare. Un prisma prende il nome dal numero dei lati del poligono di base. triangolare.
Un prisma si dice regolare se è retto e ha per basi due poligoni regolari. quadrato. triangolo equilatero. esagono regolare.
Se lo tagliamo lungo i suoi spigoli in modo da poterlo distendere su un piano, otteniamo una figura piana che si chiama sviluppo della superficie del prisma. La superficie di tutte le facce di un solido è detta superficie totale, mentre quella delle sole facce laterali è detta superficie laterale.
Il solido P è un prisma quadrangolare regolare, quindi è retto, le facce laterali sono 4 rettangoli R congruenti e le sue basi sono due quadrati Q congruenti. Qui sotto è disegnato lo sviluppo della superficie del solido P. Prova tu. Disegna lo sviluppo della superficie di un prisma triangolare regolare.
Le piramidi. faccia laterale. Si dice piramide un poliedro limitato da un poligono qualunque, detto base, e da tanti triangoli quanti sono i lati del poligono, aventi tutti un vertice comune. piramide pentagonale. piramide triangolare. piramide quadrangolare. Una piramide prende il nome dal numero di lati del poligono di base.
Una piramide si dice retta se ha per base un poligono circoscrittibile a una circonferenza, il cui centro coincide con il piede dell’altezza. Una piramide si dice regolare se è retta e se ha per base un poligono regolare. QUADRATO. PENTAGONO REGOLARE. TRIANGOLO EQUILATERO.
Il solido P è una piramide quadrangolare regolare, quindi è retta; il piede dell’altezza coincide con il centro della circonferenza inscritta nel poligono di base. Le sue facce laterali sono. quattro triangoli T isosceli congruenti, la sua base è un quadrato Q. Prova tu. • Quante sono le facce laterali di una piramide regolare esagonale ……. Ogni faccia è un triangolo: di che tipo rispetto ai lati …………………….. 6. isoscele.
Un poliedro si dice regolare se: tutte le sue facce sono poligoni regolari congruenti; tutti gli angoli diedri, formati da facce adiacenti, sono congruenti. Tetraedro regolare. 4 facce. (triangoli equilateri) 4 vertici, 6 spigoli. Dodecaedro regolare. 12 facce (pentagoni regolari) 20 vertici, 30 spigoli. Cubo. (esaedro regolare) 6 facce (quadrati) 8 vertici, 12 spigoli. Icosaedro regolare. 20 facce (triangoli equilateri) 12 vertici, 30 spigoli. Ottaedro regolare. 8 facce. (triangoli equilateri) 6 vertici, 12 spigoli.
• Un poliedro è un delimitato da posti in diversi e disposti in modo che ognuno dei lati sia comune a di essi. Indicando con V il numero di , con F quello delle e con S quello degli , la relazione di Eulero stabilisce che: V + F − S = solido. piani. due. vertici. facce. spigoli. 2. poligoni. • Osserva la figura del poliedro e inserisci i nomi che indicano le sue parti. Determina il numero di spigoli, vertici e facce del poliedro in figura e verifica per questo la relazione di Eulero. faccia. vertice. spigolo. S = 12. V = 6. F = − 12 = 2.
Una piramide si dice se ha per base un e il piede dell’altezza coincide. con il centro della circonferenza circoscritta. Una piramide si dice se è e ha per base un regolare. retta. poligono regolare. poligono circoscrivibile. • Traccia le altezze delle seguenti piramidi e stabilisci quale delle tre è regolare e quale è retta: ………….. retta. regolare.
cilindri. cono. sfera. Facendo ruotare di 360° una figura piana intorno a una. retta (detta asse di rotazione) otteniamo i solidi di rotazione. Non tutti i solidi rotondi sono solidi di rotazione.
Ruotando di 360° un triangolo rettangolo attorno a uno dei suoi cateti, si genera un cono retto. Ruotando di 360° un semicerchio attorno al suo diametro, si genera una sfera.
È sempre possibile ottenere lo sviluppo della superficie di un cilindro o di un cono. cilindro retto. cono. retto.
• Collega il nome dei diversi solidi con la figura piana che li genera (ruotando di 360° attorno a un proprio lato) e con l’opportuno sviluppo della superficie. Perché gli sviluppi delle superfici sono soltanto 2 1), b) 3),a) 2)
SOLIDI DI ROTAZIONE SI OTTENGONO FACENDO RUOTARE UN POLIGONO, PER 3600, INTORNO AD UN SUO LATO
CILINDRO RETTO. ASSE DI ROTAZIONE. RAGGIO DI BASE.
CONO. APOTEMA. ASSE DI ROTAZIONE. RAGGIO DI BASE.
INTORNO A QUALE LATO E’ AVVENUTA LA ROTAZIONE
LA PARABOLA E LA SUA EQUAZIONE. I SOLIDI. / CALCOLO DELLE AREE. DEFINIZIONE. Superficie di un poliedro. La superficie di un poliedro è la somma delle superfici di tutte le sue facce. Scomponendo un solido (anche non poliedrico) è possibile calcolarne la superficie laterale: Al = 2p . h. Al = π . r . a. Ricordiamo che alla superficie laterale va aggiunta la superficie delle basi. 32.
LA PARABOLA E LA SUA EQUAZIONE. /15. TEOREMA. Volume del cubo. La misura del volume del cubo è uguale alla misura del suo spigolo elevato alla terza potenza: V = a3. TEOREMA. Volume del prisma. La misura del volume del prisma è uguale al prodotto della misura dell’area di base per la misura dell’altezza: V = Ab . h. TEOREMA. Volume del cilindro. La misura del volume del cilindro è uguale ap prodotto dell’area del cerchio di base per la misura dell’altezza: V =π .r2 . h. Vediamo che, in generale, il volume delle tre figure può essere espresso come prodotto tra l’area della superficie di base e l’altezza. 33.
LA PARABOLA E LA SUA EQUAZIONE. I SOLIDI. / CALCOLO DEI VOLUMI. Volume della piramide e volume del cono. La piramide e il cono sono equivalenti, rispettivamente, alla terza parte di un prisma o di un cilindro di base equivalente. Quindi: TEOREMA. Volume della piramide. La misura del volume di una piramide è uguale alla terza parte del prodotto della misura dell’area di base per la misura dell’altezza: V =⅓.Ab . h. TEOREMA. Volume del cono. La misura del volume di un cono è uguale alla terza parte del prodotto della misura dell’area del cerchio per la misura dell’altezza. V =⅓.Ab . h. 34.
Al = Pb x h. Ac. C. Al. Al = C x h. Al = 2πrh. Ab. Pb = C. At = Al + 2Ab. At = 2πrh + 2πr2. At = 2πr x ( r + h ) Area cerchio. Superficie del cilindro.
At = πr x ( a + r ) Superficie del cono.
Volume del cono 1 2 h1 = h2 Ab1 = Ab2 V1 = V2 VOLUME DEL CONO V = πr2 x h 3
… ma, aumentando il numero di lati delle facce di un poliedro regolare, si approssima sempre meglio una sfera… Quindi, la sfera è un solido di rotazione o un poliedro 39.
LA PARABOLA E LA SUA EQUAZIONE. /15. Area della sfera. La misura dell’area della superficie sferica è uguale a quattro volte quella del suo cerchio massimo: Ssfera = 4 π r2. Riscrivendo l’espressione della superficie sferica come Ssfera=2πr . 2r, troviamo che la superficie di una sfera è equivalente alla superficie laterale del suo cilindro circoscritto. 40.
LA PARABOLA E LA SUA EQUAZIONE. I SOLIDI. / CALCOLO DEI VOLUMI. TEOREMA. Volume della sfera. La misura del volume di una sfera è uguale al prodotto di (4/3 π) per la misura del raggio della sfera elevaro al cubo: V =4/3 . π. r
5. CALCOLO DEI VOLUMI LA PARABOLA E LA SUA EQUAZIONE /15 42
CLASSIFICAZIONE. DELLE FIGURE SOLIDE. PER ANDARE AVANTI. FAI UN CLIC CON IL TASTO SINISTRO DEL MOUSE.
Osserva i solidi geometrici disegnati. sfera. POLIEDRI. Se consideriamo le loro facce. alcuni solidi sono limitati da SUPERFICI PIANE. alcuni da SUPERFICI PIANE e da SUPERFICI CURVE. uno di essi da una sola SUPERFICIE CURVA : la sfera. Circondiamo con una linea rossa tutti i solidi delimitati solamente da facce piane. Abbiamo formato l’insieme dei POLIEDRI.
Quelli che hanno una sola base di appoggio: le PIRAMIDI. Quelli che hanno due basi di appoggio CONGRURENTI e PARALLELE. Circondiamo con una linea rossa tutti i poliedri che hanno. due basi congruenti e parallele. Abbiamo formato l’insieme dei PRISMI.
I PRISMI. PARALLELEPIPEDI. Circondiamo con una linea rossa tutti i prismi che hanno per basi dei parallelogrammi. Abbiamo formato l’insieme dei PARALLELEPIPEDI.
SOLIDI GEOMETRICI. POLIEDRI. NON POLIEDRI. PIRAMIDI. PRISMI. PARALLELEPIPEDI. CUBO.
I solidi che hanno superfici curve vengono chiamati solidi rotondi.
Si dice poliedro un solido delimitato da poligoni, situati su piani diversi e disposti in modo che ognuno dei lati sia comune a due di essi. I poligoni si dicono facce del poliedro; i loro lati si dicono spigoli del poliedro. due facce con uno spigolo comune si dicono facce adiacenti. i loro vertici si dicono vertici del poliedro;
LA PARABOLA E LA SUA EQUAZIONE. /15. DEFINIZIONE. Poliedro. Un poliedro è una figura solida limitata da un numero finito di poligoni appartenenti a piani diversi e tali che il piano di ogni poligono non attraversi il solido. Prisma. La distanza fra il vertice (o la base superiore) e il piano della base (inferiore) si chiama altezza. L’altezza delle facce laterali di una piramide retta è detta apotema. Piramide. 9.
LA PARABOLA E LA SUA EQUAZIONE. /15. DEFINIZIONE. Poliedro regolare. Un poliedro si dice regolare quando le sue facce sono poligoni regolari congruenti e anche i suoi angoloidi e i suoi diedri sono congruenti. DEFINIZIONE. Solido di rotazione. Si chiama solido di rotazione un solido generato dalla rotazione di una figura piana intorno a una retta r. 10.
Osserviamo il poliedro della figura a fianco. Indichiamo con: • V il numero dei vertici. • F il numero delle facce. • S il numero degli spigoli. Osserviamo che per tutti i poliedri vale la seguente relazione: Relazione di Eulero. V + F − S = 2. o anche V + F = S + 2.
I vertici sono 12 e le facce 8. Sostituiamo i numeri che conosciamo nella relazione di Eulero: V + F = S = S + 2. Il numero degli spigoli è: S = − 2 = 18. Prova tu. • Quanti spigoli ha un poliedro con 6 facce e 8 vertici ……………………………. V + F = S + 2. S = V + F − 2 S = − 2 = 12. Il poliedro ha 12 spigoli.
Si chiama prisma un poliedro delimitato da due poligoni congruenti, detti basi, situati su piani paralleli e da tanti parallelogrammi quanti sono i lati di ciascuno dei due poligoni. pentagonale. quadrangolare. Un prisma prende il nome dal numero dei lati del poligono di base. triangolare.
Un prisma si dice regolare se è retto e ha per basi due poligoni regolari. quadrato. triangolo equilatero. esagono regolare.
Se lo tagliamo lungo i suoi spigoli in modo da poterlo distendere su un piano, otteniamo una figura piana che si chiama sviluppo della superficie del prisma. La superficie di tutte le facce di un solido è detta superficie totale, mentre quella delle sole facce laterali è detta superficie laterale.
Il solido P è un prisma quadrangolare regolare, quindi è retto, le facce laterali sono 4 rettangoli R congruenti e le sue basi sono due quadrati Q congruenti. Qui sotto è disegnato lo sviluppo della superficie del solido P. Prova tu. Disegna lo sviluppo della superficie di un prisma triangolare regolare.
Le piramidi. faccia laterale. Si dice piramide un poliedro limitato da un poligono qualunque, detto base, e da tanti triangoli quanti sono i lati del poligono, aventi tutti un vertice comune. piramide pentagonale. piramide triangolare. piramide quadrangolare. Una piramide prende il nome dal numero di lati del poligono di base.
Una piramide si dice retta se ha per base un poligono circoscrittibile a una circonferenza, il cui centro coincide con il piede dell’altezza. Una piramide si dice regolare se è retta e se ha per base un poligono regolare. QUADRATO. PENTAGONO REGOLARE. TRIANGOLO EQUILATERO.
Il solido P è una piramide quadrangolare regolare, quindi è retta; il piede dell’altezza coincide con il centro della circonferenza inscritta nel poligono di base. Le sue facce laterali sono. quattro triangoli T isosceli congruenti, la sua base è un quadrato Q. Prova tu. • Quante sono le facce laterali di una piramide regolare esagonale ……. Ogni faccia è un triangolo: di che tipo rispetto ai lati …………………….. 6. isoscele.
Un poliedro si dice regolare se: tutte le sue facce sono poligoni regolari congruenti; tutti gli angoli diedri, formati da facce adiacenti, sono congruenti. Tetraedro regolare. 4 facce. (triangoli equilateri) 4 vertici, 6 spigoli. Dodecaedro regolare. 12 facce (pentagoni regolari) 20 vertici, 30 spigoli. Cubo. (esaedro regolare) 6 facce (quadrati) 8 vertici, 12 spigoli. Icosaedro regolare. 20 facce (triangoli equilateri) 12 vertici, 30 spigoli. Ottaedro regolare. 8 facce. (triangoli equilateri) 6 vertici, 12 spigoli.
• Un poliedro è un delimitato da posti in diversi e disposti in modo che ognuno dei lati sia comune a di essi. Indicando con V il numero di , con F quello delle e con S quello degli , la relazione di Eulero stabilisce che: V + F − S = solido. piani. due. vertici. facce. spigoli. 2. poligoni. • Osserva la figura del poliedro e inserisci i nomi che indicano le sue parti. Determina il numero di spigoli, vertici e facce del poliedro in figura e verifica per questo la relazione di Eulero. faccia. vertice. spigolo. S = 12. V = 6. F = − 12 = 2.
Una piramide si dice se ha per base un e il piede dell’altezza coincide. con il centro della circonferenza circoscritta. Una piramide si dice se è e ha per base un regolare. retta. poligono regolare. poligono circoscrivibile. • Traccia le altezze delle seguenti piramidi e stabilisci quale delle tre è regolare e quale è retta: ………….. retta. regolare.
cilindri. cono. sfera. Facendo ruotare di 360° una figura piana intorno a una. retta (detta asse di rotazione) otteniamo i solidi di rotazione. Non tutti i solidi rotondi sono solidi di rotazione.
Ruotando di 360° un triangolo rettangolo attorno a uno dei suoi cateti, si genera un cono retto. Ruotando di 360° un semicerchio attorno al suo diametro, si genera una sfera.
È sempre possibile ottenere lo sviluppo della superficie di un cilindro o di un cono. cilindro retto. cono. retto.
• Collega il nome dei diversi solidi con la figura piana che li genera (ruotando di 360° attorno a un proprio lato) e con l’opportuno sviluppo della superficie. Perché gli sviluppi delle superfici sono soltanto 2 1), b) 3),a) 2)
SOLIDI DI ROTAZIONE SI OTTENGONO FACENDO RUOTARE UN POLIGONO, PER 3600, INTORNO AD UN SUO LATO
CILINDRO RETTO. ASSE DI ROTAZIONE. RAGGIO DI BASE.
CONO. APOTEMA. ASSE DI ROTAZIONE. RAGGIO DI BASE.
INTORNO A QUALE LATO E’ AVVENUTA LA ROTAZIONE
LA PARABOLA E LA SUA EQUAZIONE. I SOLIDI. / CALCOLO DELLE AREE. DEFINIZIONE. Superficie di un poliedro. La superficie di un poliedro è la somma delle superfici di tutte le sue facce. Scomponendo un solido (anche non poliedrico) è possibile calcolarne la superficie laterale: Al = 2p . h. Al = π . r . a. Ricordiamo che alla superficie laterale va aggiunta la superficie delle basi. 32.
LA PARABOLA E LA SUA EQUAZIONE. /15. TEOREMA. Volume del cubo. La misura del volume del cubo è uguale alla misura del suo spigolo elevato alla terza potenza: V = a3. TEOREMA. Volume del prisma. La misura del volume del prisma è uguale al prodotto della misura dell’area di base per la misura dell’altezza: V = Ab . h. TEOREMA. Volume del cilindro. La misura del volume del cilindro è uguale ap prodotto dell’area del cerchio di base per la misura dell’altezza: V =π .r2 . h. Vediamo che, in generale, il volume delle tre figure può essere espresso come prodotto tra l’area della superficie di base e l’altezza. 33.
LA PARABOLA E LA SUA EQUAZIONE. I SOLIDI. / CALCOLO DEI VOLUMI. Volume della piramide e volume del cono. La piramide e il cono sono equivalenti, rispettivamente, alla terza parte di un prisma o di un cilindro di base equivalente. Quindi: TEOREMA. Volume della piramide. La misura del volume di una piramide è uguale alla terza parte del prodotto della misura dell’area di base per la misura dell’altezza: V =⅓.Ab . h. TEOREMA. Volume del cono. La misura del volume di un cono è uguale alla terza parte del prodotto della misura dell’area del cerchio per la misura dell’altezza. V =⅓.Ab . h. 34.
Al = Pb x h. Ac. C. Al. Al = C x h. Al = 2πrh. Ab. Pb = C. At = Al + 2Ab. At = 2πrh + 2πr2. At = 2πr x ( r + h ) Area cerchio. Superficie del cilindro.
At = πr x ( a + r ) Superficie del cono.
Volume del cono 1 2 h1 = h2 Ab1 = Ab2 V1 = V2 VOLUME DEL CONO V = πr2 x h 3
… ma, aumentando il numero di lati delle facce di un poliedro regolare, si approssima sempre meglio una sfera… Quindi, la sfera è un solido di rotazione o un poliedro 39.
LA PARABOLA E LA SUA EQUAZIONE. /15. Area della sfera. La misura dell’area della superficie sferica è uguale a quattro volte quella del suo cerchio massimo: Ssfera = 4 π r2. Riscrivendo l’espressione della superficie sferica come Ssfera=2πr . 2r, troviamo che la superficie di una sfera è equivalente alla superficie laterale del suo cilindro circoscritto. 40.
LA PARABOLA E LA SUA EQUAZIONE. I SOLIDI. / CALCOLO DEI VOLUMI. TEOREMA. Volume della sfera. La misura del volume di una sfera è uguale al prodotto di (4/3 π) per la misura del raggio della sfera elevaro al cubo: V =4/3 . π. r
5. CALCOLO DEI VOLUMI LA PARABOLA E LA SUA EQUAZIONE /15 42

How To Add Offline & Online Videos in PowerPoint 2013
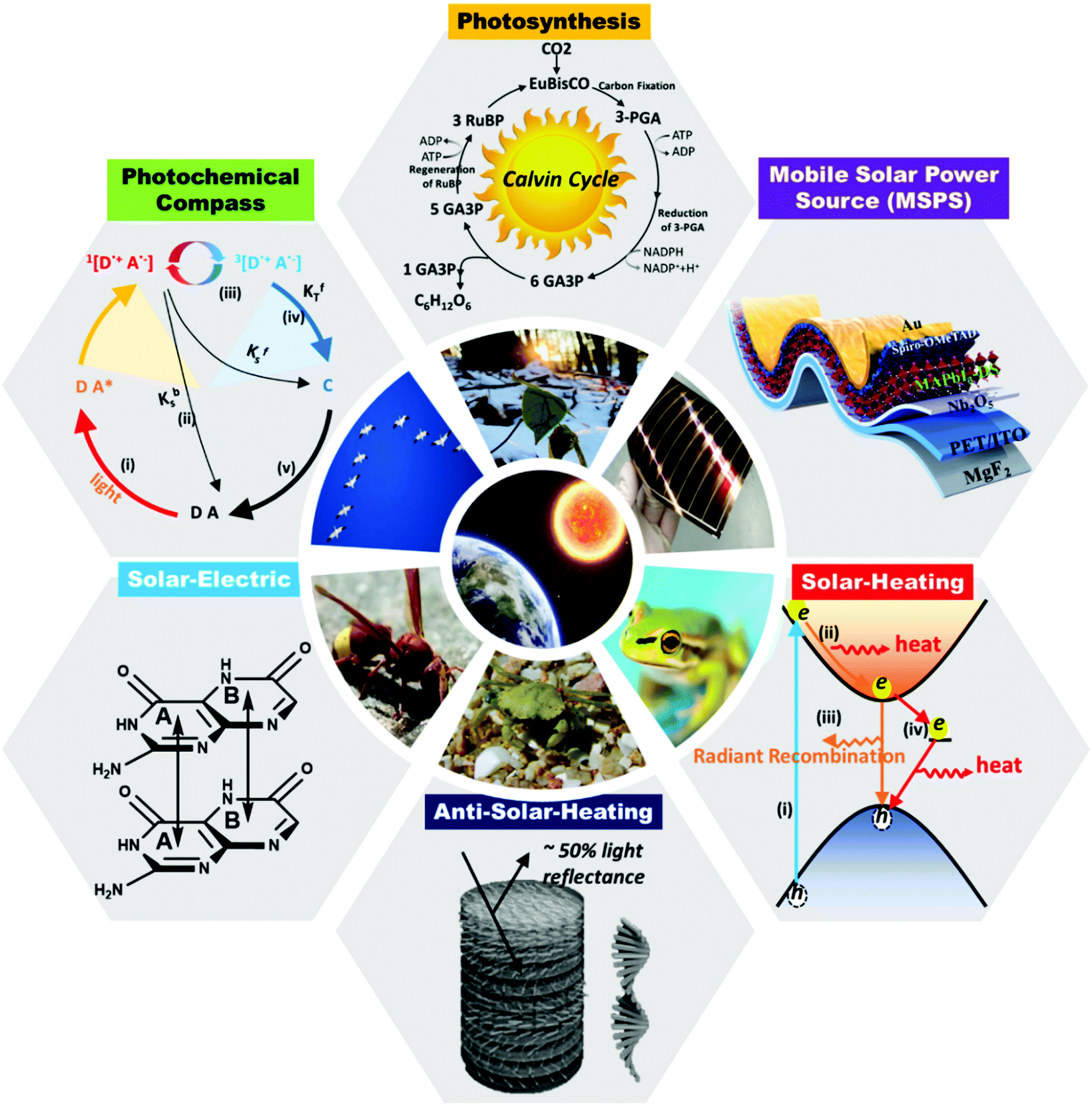
Bio-inspired strategies for next-generation perovskite solar

3D Printing of Na1.3Al0.3Ti1.7(PO4)3 Solid Electrolyte via Fused

Methylhydrazinium]2PbCl4, a Two-Dimensional Perovskite with Polar

I solidi. - ppt video online scaricare

Applied Sciences, Free Full-Text

How To Convert Powerpoint To Video Without Any Software?

Interface engineering for single-molecule devices: Trends in Chemistry

How to make video using Power point presentation

Symmetries in transmission electron microscopy imaging of crystals

Ab initio study of defect interactions between the negatively
PowerPoint Cannot Play Media: How to Play Video Smoothly
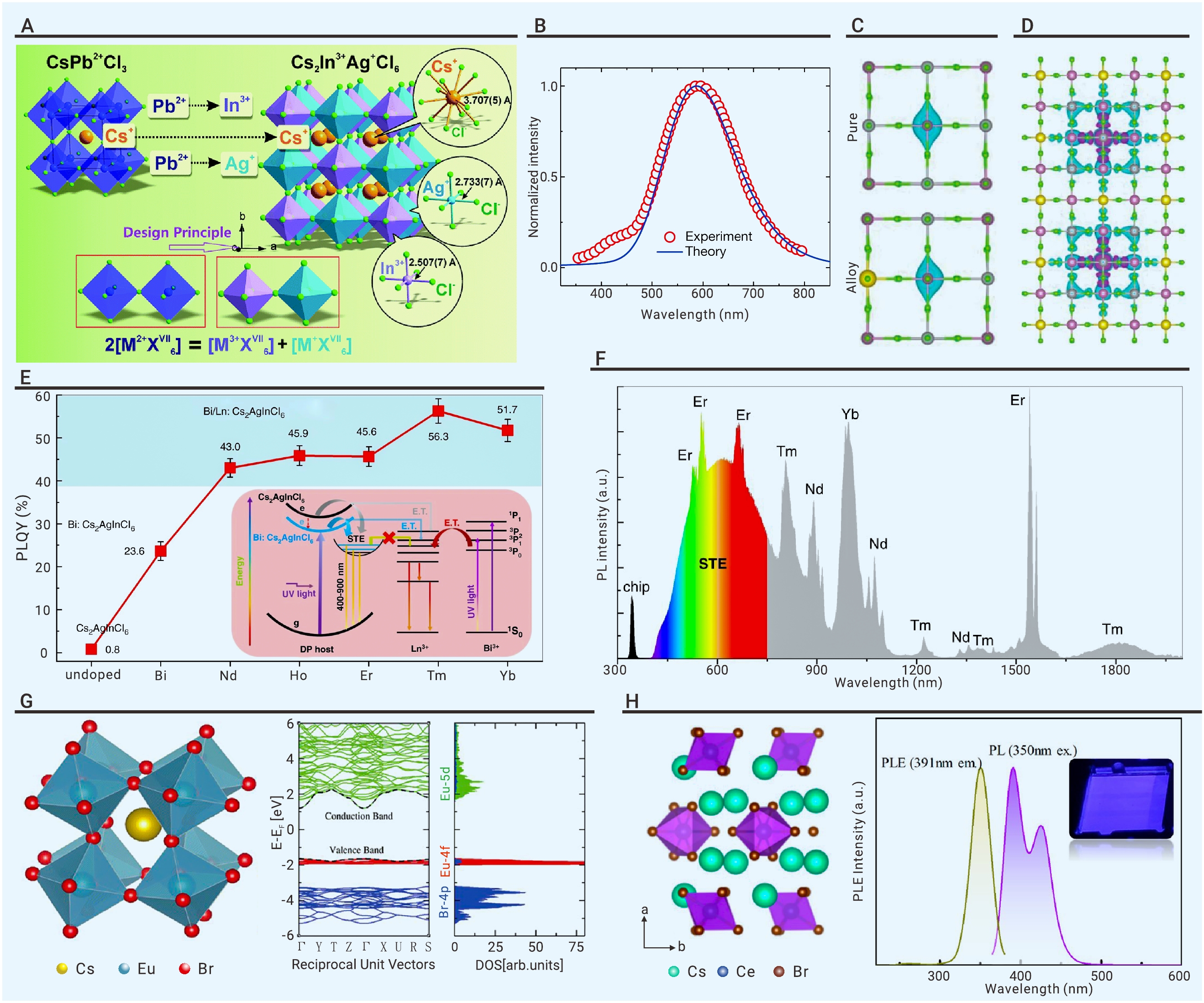
Opportunity of lead-free metal halide perovskites for
raccomandato per te
 I Solidi Geometrici: Esercizi per la Scuola Primaria14 Jul 2023
I Solidi Geometrici: Esercizi per la Scuola Primaria14 Jul 2023 I Solidi Geometrici: Esercizi per la Scuola Primaria - SostegnO 2.014 Jul 2023
I Solidi Geometrici: Esercizi per la Scuola Primaria - SostegnO 2.014 Jul 2023 I Solidi Geometrici: Esercizi per la Scuola Primaria14 Jul 2023
I Solidi Geometrici: Esercizi per la Scuola Primaria14 Jul 2023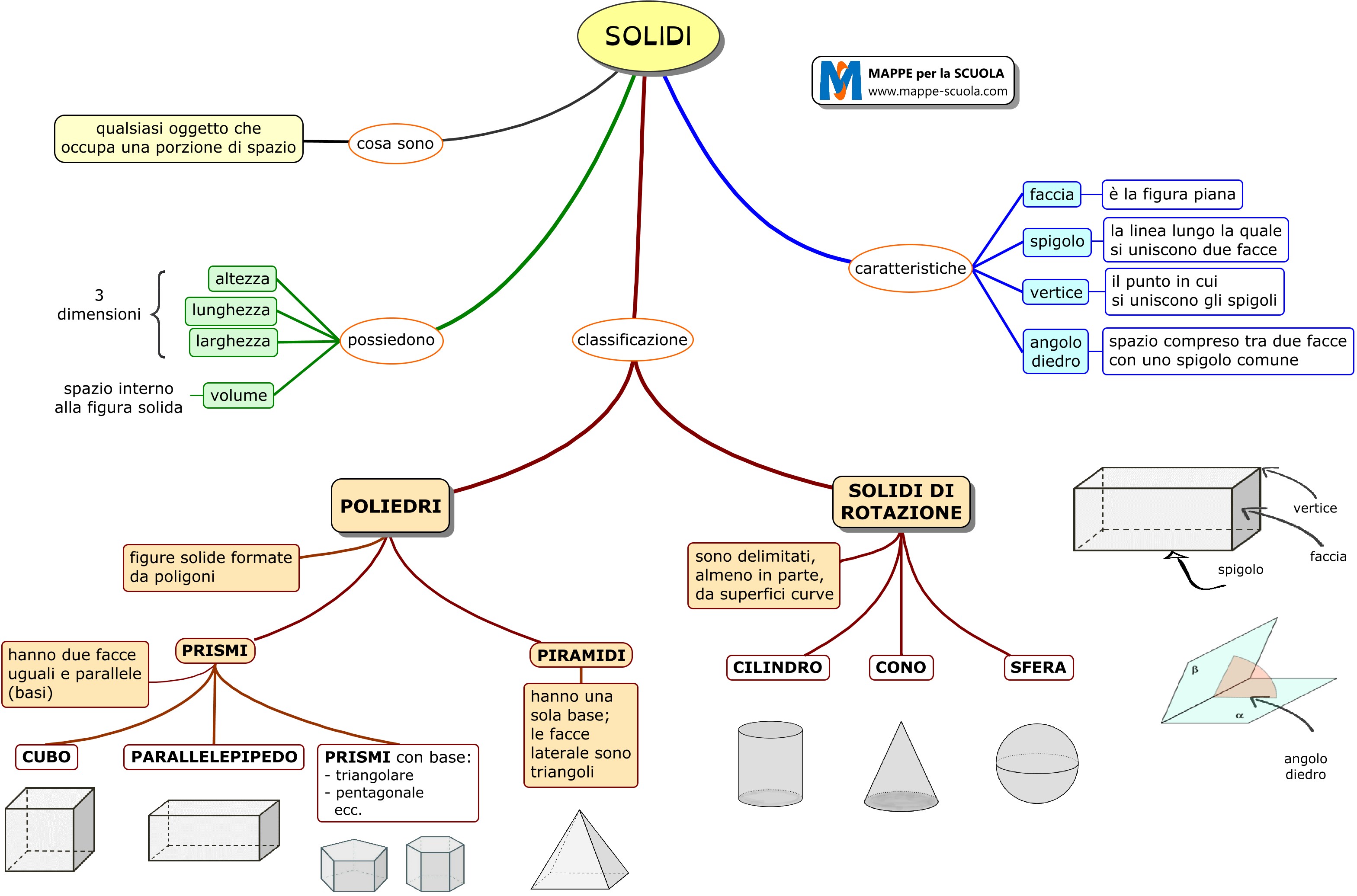 SOLIDI - Mappe per la Scuola14 Jul 2023
SOLIDI - Mappe per la Scuola14 Jul 2023 Solidi geometrici14 Jul 2023
Solidi geometrici14 Jul 2023 Come costruire i solidi. Geometria scuola primaria14 Jul 2023
Come costruire i solidi. Geometria scuola primaria14 Jul 2023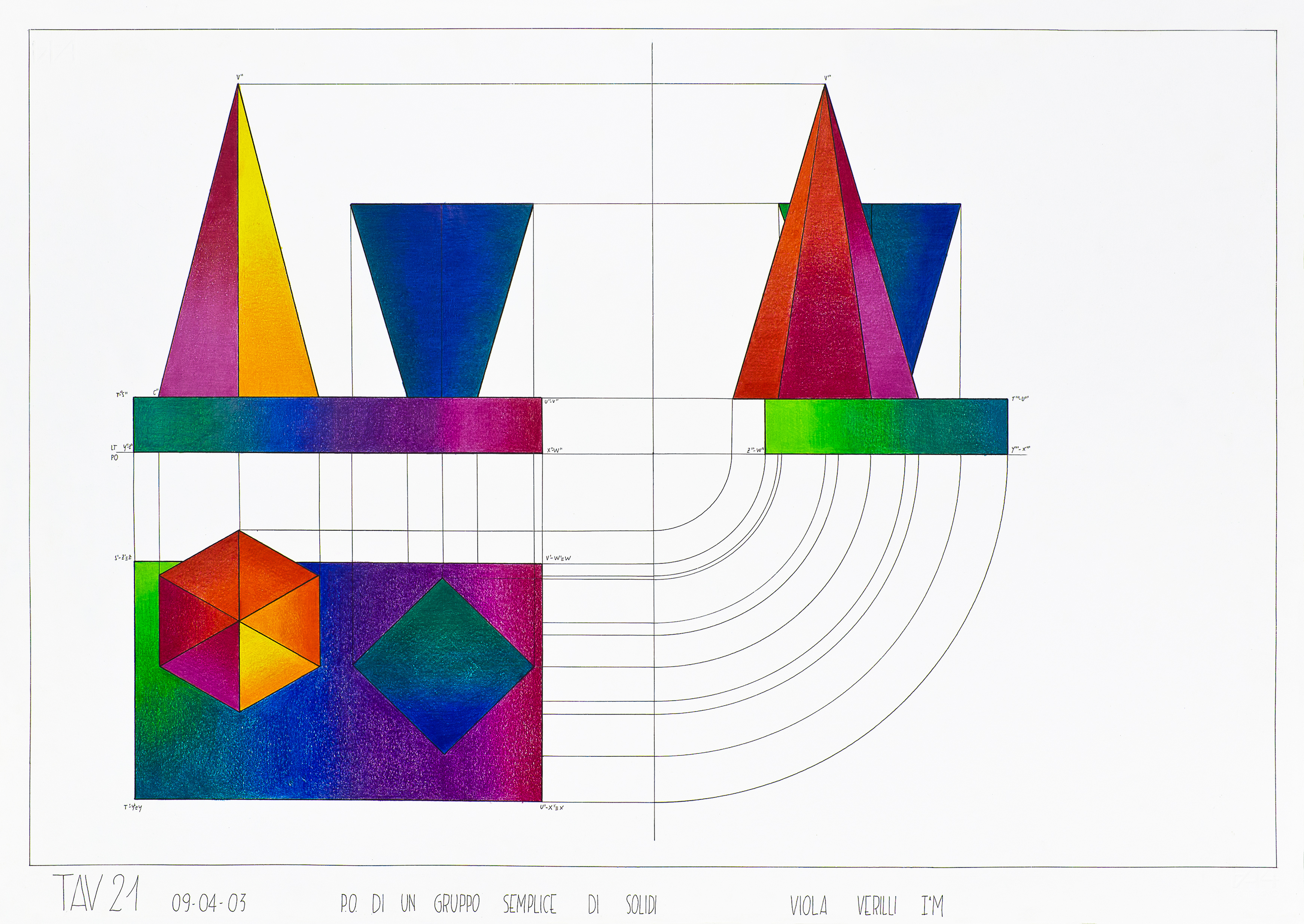 P.O. di solidi geometrici « Fava – Geometria e disegno14 Jul 2023
P.O. di solidi geometrici « Fava – Geometria e disegno14 Jul 2023- ♥ SOLIDI GEOMETRICI RICO IN PLEXIGLASS VINTAGE CON SCATOLA DIDATTICA SCUOLA14 Jul 2023
 Solidi geometrici trasparenti - 12 pezzi14 Jul 2023
Solidi geometrici trasparenti - 12 pezzi14 Jul 2023 Laboratorio di geometria solida14 Jul 2023
Laboratorio di geometria solida14 Jul 2023
Potrebbe piacerti anche
 Contenitori Plastica Con Coperchio14 Jul 2023
Contenitori Plastica Con Coperchio14 Jul 2023- MD WebStore - Super Saldo! 🤩 La #Lavatrice Atlantic14 Jul 2023
 CONFETTI PAPA: vendita ingrosso14 Jul 2023
CONFETTI PAPA: vendita ingrosso14 Jul 2023 Gancio portacacciaviti per pannelli portautensili14 Jul 2023
Gancio portacacciaviti per pannelli portautensili14 Jul 2023 500W Impastatrice Planetaria Professionale,3 Velocità Basso Rumore14 Jul 2023
500W Impastatrice Planetaria Professionale,3 Velocità Basso Rumore14 Jul 2023- Quali personaggi ha copiato la Marvel dalla DC Comics? - Quora14 Jul 2023
 MSPORTS Tappetino da Ginnastica Premium 190 x 100 x 1,5 cm con Cinturino14 Jul 2023
MSPORTS Tappetino da Ginnastica Premium 190 x 100 x 1,5 cm con Cinturino14 Jul 2023 Cubo di Rubik's Master 4x4 Spin Master 6064639 - Baby Planet Shop Online14 Jul 2023
Cubo di Rubik's Master 4x4 Spin Master 6064639 - Baby Planet Shop Online14 Jul 2023 Piccone Che È Uno Strumento Di Scavo Del Terreno Utilizzato Per14 Jul 2023
Piccone Che È Uno Strumento Di Scavo Del Terreno Utilizzato Per14 Jul 2023 Nuxe must-have products gift set - Shop online at14 Jul 2023
Nuxe must-have products gift set - Shop online at14 Jul 2023

